Empecemos con un tema básico llevado a la practica; esta es una práctica que desarrolle en clase sobre error en las mediciones.
INTRODUCCIÓN
Los resultados de las
medidas nunca se corresponden con los valores reales de las magnitudes a medir,
sino que, en mayor o menor extensión, son defectuosos, es decir, están
afectados de error. Las causas que motivan tales desviaciones pueden ser
debidas al observador, al aparato o incluso a las propias características del
proceso de medida. Un ejemplo de error debido al observador es el llamado error
de paralaje que se presenta cuando la medida se efectúa mediante la lectura
sobre una escala graduada. La situación del observador respecto de dicha escala
influye en la posición de la aguja indicadora según sea vista por el
observador. Por ello para evitar este tipo de error es preciso situarse en
línea con la aguja, pero perpendicularmente al plano de la escala. Otros
errores debidos al observador pueden introducirse por descuido de éste, por
defectos visuales, etc. Así, cuando se desea medir la tensión eléctrica
existente entre dos puntos de un circuito con un voltímetro, una parte de la
corriente se desvía por el aparato de medida, con lo que el sistema a medir
queda ligeramente perturbado. De igual modo, al medir una temperatura con un
termómetro se está provocando una cesión o absorción de calor entre termómetro
y sistema hasta que se alcanza el equilibrio térmico entre ambos. En un cierto
grado, el valor de la temperatura a medir se ha visto modificado al hacer
intervenir el aparato de medida.
Como consecuencia de la
existencia de diferentes fuentes de error, el científico se plantea por sistema
hasta qué punto o en qué grado los resultados obtenidos son fiables, esto es, digno
de confianza. Por ello, al resultado de una medida se le asocia un valor
complementario que indica la calidad de la medida o su grado de precisión. Los
errores o imprecisiones en los resultados se expresan matemáticamente bajo dos
formas que se denominan error absoluto y error relativo.
1.1. ERRORES SISTEMÁTICOS:
Son aquellos que se
repiten debido a un defecto en el instrumento de medida ó a un defecto de lectura del
observador. Por ejemplo:
•
Errores en
la calibración del instrumento
•
Errores del
observador
•
Errores de
imperfecciones del método de medida
1.2. ERRORES ESTADÍSTICOS:
Son aquellos inherentes al método de medida
cuya presencia sólo
está
regida por las leyes de la probabilidad. Por ejemplo:
•
Errores en
la estimación de la fracción de la menor división de una
escala
•
Errores
debidos a condiciones fluctuantes
•
Errores de
definición de objetos
2. CÁLCULO DE ERRORES
2.1. MEDIDAS DIRECTAS
2.1. MEDIDAS DIRECTAS
Supongamos que se efectúa n medidas
de x
• El valor más probable:
Xp = ____________________________________
n
• El error absoluto (∆x):
• Resultado:
X = Xp ± ∆X
• El error relativo:
• El error
relativo porcentual:
E% = error absoluto X 100
II. OBJETIVOS
Determinar errores sistemáticos y
estadísticos
en la medida de magnitudes físicas
relacionadas con fenómenos biológicos.
III. MATERIALES Y EQUIPOS
•
01 termómetro clínico - 01 balanza
•
01 cronómetro
•
01 cinta métrica
IV.
PROCEDIMIENTO
1.
TEMPERATURA CORPORAL
Para tomar
la temperatura corporal se limpia el termómetro y se sacude hasta que la
temperatura este por debajo de 34 ºC. Luego, se coloca el termómetro en la
axila no menos de 5 min, se lee la temperatura y se anota en la
Tabla I. Repetir el procedimiento en intervalos de tiempo que permita tener 10
medidas durante el tiempo de la práctica.
TABLA
I
|
N
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
f(min)
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
5
|
|
T
(ºC)
|
35,8
|
36,1
|
35,6
|
35,5
|
35,0
|
35,4
|
36,5
|
35,7
|
36,4
|
35,6
|
2. SUPERFICIE CORPORAL
Mide el peso y talla de un estudiante y anote
estas medidas en la Tabla II.
Luego, use la fórmula
de Du
Bois para determinar la superficie corporal
W es
el peso en kgf, h es la talla en cm y S la superficie en m2.
TABLA II
|
n
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
W
(kgf)
|
50,5
|
49,5
|
50
|
50
|
50,5
|
50,5
|
50,5
|
50
|
50,5
|
49,5
|
|
Mcm)
|
155
|
155
|
156
|
155
|
155
|
156
|
156
|
56
|
155
|
155
|
|
S (m2)
|
1,47
|
1,46
|
1,47
|
1.47
|
1,47
|
1,48
|
1,48
|
1,47
|
1.47
|
1,46
|
V.
RESULTADOS (FUNDAMENTACIÓN)
1.
¿Qué diferencia
hay entre instrumentos de medida analógicos y digitales? ¿Quién calibra a quién?
En general los parámetros que
caracterizan un fenómeno pueden clasificarse en Analógicos y Digitales, se dice
que un parámetro es analógico cuando puede tomar todos los valores posibles en
forma continua, por ejemplo: el voltaje de una batería, la intensidad de luz,
la velocidad de un vehículo, la inclinación de un plano, etc.
Por otra parte se dice que un
parámetro es digital cuando solo puede tomar valores discretos, por ejemplo: el
número de partículas emitidas por un material radioactivo en un segundo, el
número de moléculas, en un volumen dado de cierto material, el número de
revoluciones de un motor en un minuto, etc(1).
-Instrumentos
Analógicos e Instrumentos Digitales
Instrumentos Analógicos.
El
término: Analógico Se refiere a las magnitudes o valores que varían con el
tiempo en forma continua como la distancia y la temperatura, la velocidad, que
podrían variar muy lento o muy rápido como un sistema de audio.
En la vida cotidiana el tiempo se representa en forma analógica
por relojes (de agujas), y en forma discreta (digital) por displays digitales
.En la tecnología analógica es muy difícil almacenar, manipular, comparar,
calcular y recuperar información con exactitud cuando esta ha sido guardada, en
cambio en la tecnología digital (computadoras, por ejemplo), se pueden hacer
tareas muy rápidamente, muy exactas, muy precisas y sin detenerse. La
electrónica moderna usa electrónica digital para realizar muchas funciones que
antes desempeñaba la electrónica analógica.
Ventajas
a) Bajo Costo.
b) En algunos casos no
requieren de energía de alimentación.
c) No requieren gran
sofisticación.
d) Presentan con
facilidad las variaciones cualitativas de los parámetros para visualizar
rápidamente si el valor aumenta o disminuye.
e) Es sencillo adaptarlos a
diferentes tipos de escalas no lineales.
Desventajas
a) Tienen poca
resolución, típicamente no proporcionan más de 3 cifras.
b) El error de paralaje
limita la exactitud a ± 0.5% a plena escala en el mejor de los casos.
c) Las lecturas se
presentan a errores graves cuando el instrumento tiene varias escalas.
d) La
rapidez de lectura es baja, típicamente 1 lectura/
segundo.
e) No pueden emplearse
como parte de un sistema de procesamiento de datos de tipo digital.
Instrumentos Digitales.
El término: Digital Se refiere a cantidades discretas como la
cantidad de personas en una sala, cantidad de libros en una biblioteca,
cantidad de autos en una zona de estacionamiento, cantidad de productos en un
supermercado, etc.
Los Sistemas digitales tienen una alta importancia en la
tecnología moderna, especialmente en la computación y sistemas de control
automático.
Ventajas
a)
Tienen alta resolución alcanzando en algunos casos más de 9 cifras en
lecturas de frecuencia y una exactitud de + 0.002%
en mediciones de voltajes.
b) No están sujetos al error de paralaje.
c) Pueden eliminar la posibilidad de errores por
confusión de escalas.
d) Tienen una rapidez de lectura que puede superar las 1000
lecturas por segundo.
e) Puede entregar información digital para procesamiento
inmediato en computadora.
Desventajas
a) El costo es elevado.
b) Son complejos en su construcción.
c) Las escalas no lineales son difíciles de introducir.
d) En todos los casos requieren de fuente de alimentación.
De las ventajas y desventajas anteriores puede observarse que para
cada aplicación hay que evaluar en función de las necesidades específicas, cual
tipo de instrumentos es el más adecuado, con esto se enfatiza que no siempre el
instrumento digital es el más adecuado siendo en algunos casos contraproducente
el uso del mismo.
Los instrumentos digitales tienden a dar la impresión de ser muy
exactos por su indicación concreta y sin ambigüedades, pero no hay que olvidar
que si su calibración es deficiente, su exactitud puede ser tanta o más mala
que la de un instrumento analógico (1).
2.
Use los datos de la Tabla I y
calcule el valor más
probable, el error absoluto, el error relativo, el error
relativo porcentual y exprese el resultado de la temperatura corporal del
estudiante seleccionado.
·
El valor más probable = promedio
Xp =
35,76 = 35,8
·
El error absoluto :
35,8-35,8 = 0
36,1-35,8=(0,3)2
= 0,09
35,6-35,8=(-0,2)2=0,04
35,5-35,8=(-0,3)2=0,09
35-35,8=(-0,8)2=0,64
35,4-35,8=(-0,4)2=0,16
36,5-35,8=(0,7)2=0,49
35,7-35,8=(-0,1)2=0,01
36,4-35,8=(0,6)2=0,36
35,6-35,8=(-0,2)2=0,04
·
Er=0,004
·
E%=0,004x100%=0,4%
·
Resultado:
X=35,8±0,15
X1=35,95
X2=35,65
3.
Con los datos de la Tabla II,
calcule el índice
de masa corporal del estudiante elegido.
El índice de
masa corporal (IMC) es
una medida de asociación entre el peso y la talla de un individuo ideada por el estadístico belga L. A. J. Quetelet, por lo que también se conoce
como índice de Quetelet.(2).
Donde:
I.M.C: Correspondiente al Índice de Masa Corporal.
Peso: Correspondiente al peso del sujeto en Kg.
Talla: Correspondiente a la estatura de sujeto en metros.
Clasificación
del I.M.C. Según la sociedad Española para el estudio de la obesidad (3).
|
Índice de masa corporal en varones
|
Índice de masa corporal en mujeres
|
Interpretación del índice de masa
corporal
|
|
Menor 20
|
Menor 20
|
Bajo peso
|
|
20 – 24,9
|
20 – 23,9
|
Normal
|
|
25 – 29,9
|
24 – 28,9
|
Obesidad leve
|
|
30 – 40
|
29 – 37
|
Obesidad severa
|
|
Mayor 40
|
Mayor 37
|
Obesidad muy severa
|
Xp= 50,15
4.- Investigue acerca de los errores aceptables en su área
específica de alguna variable medible
·
Error
en las determinaciones médicas
ü Error
de apreciación: Es el que está dado por la sensibilidad o precisión del
instrumento o método de medida. Si medimos el valor de glucemia y el método no
permite medir variaciones inferiores al miligramo por 100ml de plasma, ése será
nuestro error de apreciación igual pasa en una balanza de baño donde no podemos
apreciar valores menores a un miligramo.
ü Error
accidental: Cuando se realiza una medición, hay infinidad de factores que
pueden influenciar el valor que se obtiene. Siguiendo con el ejemplo de la
glucemia, pequeñas variaciones en los volúmenes medidos, en la calidad de algún
reactivo, o en la sensibilidad del aparato, etc,. Hacen que varias mediciones
de la misma muestra no den valores exactamente iguales (4).
Ø Error Muestral o Tolerancia de
error:
Es la
diferencia entre un estadístico y su parámetro correspondiente. Generalmente el
error máximo aceptable en medicina de alguna variable medible es 5%, en estudios de fármacos es 1%. La tolerancia debe ir
de la mano de la prevalencia del estudio en cuestión (5).
VI. CONCLUSIONES
-
Se logró determinar errores sistemáticos y
estadísticos en la medida de magnitudes físicas relacionadas con fenómenos
biológicos.
VII. REFERENCIAS BIBLIOGRÁFICAS
1.-
Todo Ingeniería Industrial. Diferencia, ventajas y desventajas de Instrumentos
analógicos y digitales. [Sede Web]. Agosto24, 2013.
2. -
Sharon A. Hoeger, Werner W. K. Hoeger.
Ejercicio y Salud. 6 ta. Ed. España: Cengage Learning Editores; 2005.
3.- Sirvent J, Garrido R. Valoración
Antropométrica de la composición corporal: Cineantropometría. España:
Universidad de Alicante; 2009.
4.-
Parisi M. Temas de biofísica. México: McGraw - Hill;
2004.
5.- Castillo L.
Bioestadística para las ciencias de la Salud. España: Capital Ediciones; 2004.





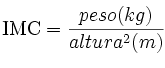
No hay comentarios:
Publicar un comentario